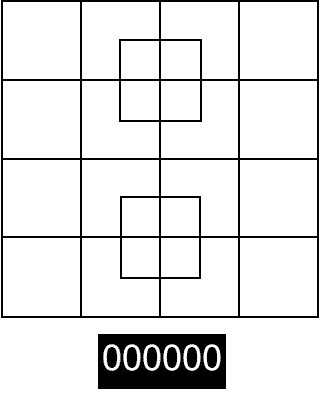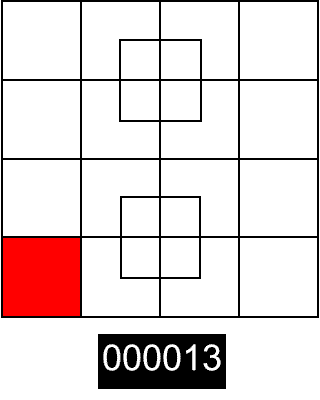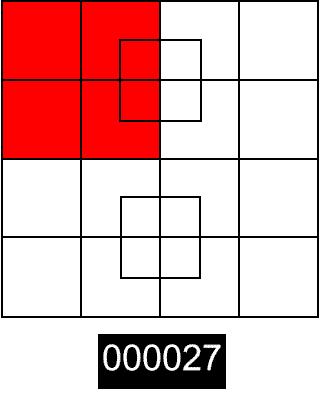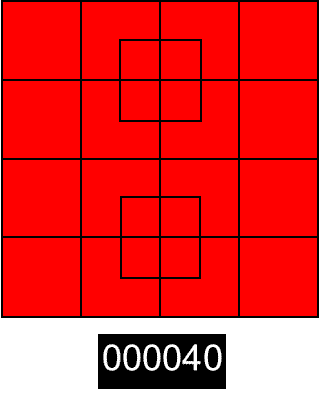
How many squares indeed
This is neither video game, nor film related but since it’s my site, I can do what I like with it.
You see, there’s this image floating around the social inter-tubes of a grid of different size squares and the question all the posters pose is “How many squares do you see?”. Some only count 24, others 32 or 36, but the correct answer is 40. And each time I answer 40, I get the same response: “I just don’t see it”.
So, either because I feel like doing a public service, or because I just want to see this dumb debate put to rest (or maybe because I figure this might be a good way to drive traffic to our modest little site), please join with me in counting the flashing red squares:









you guys left out the smaller squares adding up to an additional square making it a total of 42 squares, how can you publish this as if it is fact and you are completely wrong lol
Are you talking about squares 17 and 18?
It was counted as 17 and 18, I guess u missed it.
Hi Michael, I’m pretty certain the two you describe are highlighted in the animation above as Jeremy pointed out. If not, grab a screenshot and color in the squares that I missed and I’ll be happy to post an update and credit your find.
Christopher,
I found the forty after a bit of mind crunching/relaxing/and rethinking. The 3×3’s escaped me for awhile. Thanks for posting the animation. Very cool. (((And you were a whole lot nicer to Michael than I would have been.)))
Thanks so much for this animation Christopher. I was trying to explain the answer of 40 to my friends. I posted some other pretty good answers on my wall, but this one anybody can follow & understand. Some insist that there are 44, but I don’t see it, & some self-proclaimed geniuses say that there are only 16 true squares because you can’t count the ones broken up by lines. I am not a genius or math expert by-far, but I think that square can be made up of smaller squares, so when it says “how many squares”, it means all, not just those with no lines.
i also see 44
You are right because the groups of squares people are saying can’t be counted because of intersecting lines is actually wrong because if you look at the perimeter of those groups, they are solid lines and haven’t been counted yet.
In the theory that is being proposed, where your counting squares not separated by lines, the answer could theoretically be an infinite number
In fact there are only 16 true squares. All the other squares shown actually have lines going through them therefore making them not perfect squares. But that’s my opinion, probably thinking too much inside the box instead of outside.
Christal – I agree but don’t classify myself as a genius. The way I see the graphic once you count past 16 you are counting squares that have already been counted .. that is if you are willing to accept the premise that a “square” can have intersecting lines.
Between any two points there are an infinite number of intersecting lines at infinite different angles.
It doesn’t matter if there is a line going through it, it is still a square.
Bizarre definitions of squares going on here. People clearly didn’t pay any attention in geometry. The fact that there are intersecting lines on a plane does not mean that a plane figure with four equal straight sides and four right angles isn’t still a square. It’s amazing to me that people are clearly and graphically shown the answer to a fairly simple puzzle and they still want to make bizarre arguments.
Cristal, I agree with you, 16 true squares. Other than that you are adding in theoretical lines, and your just complicating things, overthinking it, then you can come up with an infinite number of squares. So depending on your school of thought, I say, being the genius that I am, (lolol) the true answer ius 16, or the only other alternative is infinite number of squaresl. That is my final answer! lol
Still baffled by the nit-picking. It’s like saying a pair of dice aren’t cubes because they have spots on the sides.
cool animation
but it does not highlight the 40th square being the entire outside square.
Frank. Sure it does. It’s the very last one highlighted.
what are you talking about? which “smaller squares”? put a graphics up somewhere, smartie
No, they counted those.
Thank you! I thought I got ’em all but missed 4
If you are referring to the two sets of four squares that make two squares, I counted those when I got 40. If you are getting more than forty, you are probably counting some squares more than once or including rectangles.
do you always count things twice?
I go 40. I’d like to know what two you are talking about :)
Idon’t see 41 & 42? Explain thoroughly please =)
why isn’t anyone counting the square that make up the whole puzzle? that would make 41.
….they did?
Brenda, they did. It was number 40. Good lord, now people can’t even watch red squares popping up on their screen. I weep for American education.
Clearly, there are squares: how do you use a simple puzzle to expose the mind to an ever expanding universe (or contracting). I think this puzzle allows the mind to focus on, not the right answer, the question. 41
Didnt you watch the answer the 2 small squares were counted after 16. Way to spout off about yourself being so wrong. Think before you speak next time!
What the hell are you talking about there are only 40 squares.
They missed nothing out, I been going over this puzzle for months, I thought it was 36, until a maths teacher showed me and gave me the answer in another link, the correct answer is 40 squares
they counted all the squares. you must be drunk…again
What are you looking at, the answer is even up there. This proves that people will argue even in the face of pure facts. it is 40 genius.
Actually he did, you retard. You counted those squares twice.
I’m not sure how you’re getting only 40. I tilt my laptop screen back and see lighter squares inside of the black bold squares. (seems like a rough draft)The total count I have is 50. When I tip my screen back, the first square does not have an inner square. The rest of the squares do have the second inner square which adds up to 30. (15 squares x 2 inner squares each=30)
Now, the 2 center squares each have 4 squares. Those 4 squares have the lighter squares inside of them. And then counting those 2 squares alone.
That total is 18.
Then we have the square at the lefthand top that does not have its’ inner square so that is counted alone. The outer square which is holding them all in.
30+18+1+1=50
I could be reading too much into it. However, the game didn’t specify what counted and what didn’t :) A square is a square is a square!
Don’t you think that “tilting your screen back” is by definition “reading too much into it”, or adding a variable that may not be consistent across different types of computer screens? Thanks for the graphical “40” explanation BTW!
Well, if you’re looking to read too much into it and get technical, this image is made of of hundreds of thousands of square pixels that make up hundreds of thousands of squares when combined, but this puzzle comes from a good old fashioned geometry puzzle, probably drawn with a good old fashioned pencil, on good old fashioned paper.
So, assuming this was a simple drawing, you would be able to trace over 40 squares using the lines laid out in the illustration.
Right On!
No Like button, so I’ll just say, LIKE.
Pixels are not square.
The third column is one pixel too wide therefore not part of any square–messes up the whole count. (Just kidding.)
Actually, thanks for posting this it helped settle our little debate. Hopefully it does bring a lot of traffic to your site.
Terrific response, Christopher.
Sorry Tracy. You’re an idiot.
If I cross my eyes I see double so there are actually 80. Ha!
LOL! Good one!
the way you are counting is going too far. what about the border, or the web page, or each pixel, or the screen? i guess with current resolution of my screen, there are about 1366×780 squares. no. there are 40 squares. 8 – 1/4 size, 18 – 1×1, 9 – 2×2, 4 – 3×3, 1 – 4×4. therefore, 18+9+8+4+1= 40. easy
You’re creating an optical illusion when you tilt your screen. Just think of this puzzle as it was when originally created on paper years ago.
I don’t think the “rough draft” squares are meant to be counted, since they don’t show up on everyone’s computer.
The lighter squares are ghost images from a poor scan of the original. Common with lower quality scanners.
The lighter squares you are seeing (and bare with me on this because it’s going to get very technical) are in fact artifacts resultings from the jpeg image compression (lossy algorithm). This occurs because jpeg algorithms tend to smooth areas where there’s high contrast transitions, thus creating the gray areas between the black lines and the white background. This helps achieving greater compression ratios but the tradeoff is loss of image quality/fidelity. That’s why jpeg is usually not a very good candidate for images with lots of text and charts (there’s lots of high contrast colors between text and backgroud; large one colored areas are not well handled). One can use lossless image formats such as png (or even jpeg but the lossless version which is not mainstreamed yet, probably due to some legal aspects related to the usage of such algorithms). Lastly, I counted 40 squares. :)
You make several good points and really aren’t far off, except for one thing…. The image is an animated GIF. :)
You know, I would have thought your comment was intelligent, but you said “bare” with me. Really? Do you want me to get naked with you? Is your comment just a big complicated come-on?
Make sure you know what words to use if you’re trying to sound smart or you will fail.
you must be drunk too…again
You seem a bit “tipsy”.
Yeah, Tracey is right, but there is even more. I counted the squares across the top of my screen I got 1366 squares, and going down there is 766. My screen even says there is that many “pixels”, whatever that means. I have lost count at 1,049,088. Genius Tracey, the answer is 40.
Tracy, what kind of hallucinogenic drugs are you using? 42 squares. You think inside the box outside of the square. Then you can see all the cubes. Since they all have lines in them then, the last 2 have lines inside them.
looks like there might be some artifacting in that image, but all you should be counting is the black outlined boxes, not any kind of anti-aliasing or negative image when you flip your screen to different angles. 40 makes sense to me.
Kimmy,
Right! 40 makes sense, and the math. Good eye!
i see a total of 43…the extras i see are at #17, #18 and #31
I call bullshit… There is, arguably, 80, not 40. The reasoning for my argument is set theory; Yes, there is 8 .5x.5 squares, yes there is 18 1×1 squares, yes there are 9 2×2 squares, and 4 3×3 squares, and 1 4×4 square, however there is also negative space which is in the shape of a square as well, this would instantly double the count. Why exclude one from being counted, and allow the other?
I looked at your video, it seems you did highlight the negative space, well alright.. instead imagine the negative space and the line segments as separate entities, to better clarify.
NO. It’s not asking to count boxes. It is asking to count squares. Squares are defined by the LINES not the negative space or Ewoks that walk on them or any other imaginary bull shit you want to stroke yourself over. There are 40 squares. This is ridiculous now.
You, sir, are my hero.
Malarkey!!!
What about the square created by using your #28 and deleting #17 from it? That adds two more…likewise, another unique square type can be formed combining your #1, #2, #3, #4, #5, #8, #9, #12, #13, #14, #15, #15…additional variations of this total 5 additional squares.
Grand Total 47 that I can find.
Whoops…small typo…should be #13, #14, #15, #16…
umm…that’s not a square, randy. that’s a toroid.a square-boundaried toroid to be sure, but it asked how many squares, not how many squares and toroids.
Point conceded! I am back to 40…and seriously considering the point that squares, technically, should not have lines through them…leaving a count at 16. Fun puzzle!
If you were to only count squares without lines through them, there would only be 8 squares, not 16. Just an observation…
I stand corrected! 40 it is! Although, someone’s point about the squares with lines going through them should technically count…an interesting point for sure. Fun puzzle!
Sheeez…”SHOULDN’T count”…not “should count”.
Wish I could reply to my own post…and I’m back to 16 “real” squares…forgot the teeny ones in the middle.
But I still think 40 is the correct answer.
Wouldn’t it be a square-boundaried annulus?
I agree with Dennis. I see 43, but i’ve been told that I’m wrong and that the only squares that should be counted are solid squares.
Dennis, 16,17, and 31 are already in the count. Why would you count them twice? Making the total still 40.
the outside of those square is another square
You wouldn’t count the outside of those ones, because they aren’t squares. You Only find SQUARES.
Trevor, I don’t think the spirit of the game is to include each square twice based on the thickness of the pencil.
You can only really count the lines, as the “negative space” is divided up by the lines. If you wanted to count negative space squares as well there are only 16 proper ones, making 56.
You missed 5. There are the four 2X2 squares in the corners and the one in the centre. So I got 45.
Oops I recounted and concede. There are 40 :)
Am I the ONLY one that counts 16 squares? A REAL square should have NO lines in the middle of it. Why am I the ONLY one that counts this as a REAL square?
THINK PEOPLE! THINK!
No, that would be 16 (though I thoroughly disagree with you on premise).
There are the 4 squares along the left side and 4 along the right to give us 8.
Then there are the 8 mini-squares.
That makes a total of 16
The definition of a square is ‘A shape having four equal length sides’. It says nothing about what is inside that shape, it only defines the sides. Therefore a square divided by any number of lines is still a square.
The answer is 40 and YOU are and Idiot.
Why am I an idiot? I was simply following his logic (he originally stated 12, I believe). I made that clear by saying, “I thoroughly disagree with you on premise.”
Now why would you call this person an idiot? Uncalled for. We are all just having fun. Apologize, my goodness.. Show some class and sportsmanship in this mind-bender game…
No, you’re not the only one in the entire world to come up with that answer. Read some of the comments, & you will see that. But I don’t agree that a square with smaller squares inside of it is no longer a square. That would mean that a checker board is not a square because it has smaller squares inside of it. What would you call the shape of a checker board? I could not find anything supporting your claim. Please post a link proving that a square is not a square if it has lines through it. And I think that your cocky, superior attitude sucks! Like you’re a genius & the rest of us are slumped over dragging our hairy fingers across the ground.
Why so serious? lol
If a line is inside a square, then that square is broken up. Sure it’s still technically a square, but the INSIDE is NO LONGER a square.
But, remember this, there seems to be no rules for this game, so actually no one is right. Which is actually quite stupid, because brainteazers should have a logical answer. But, ones like this one open up discussion, which is fun. I was having FUN with my comments, but people like you take them too serious. I was serious about my answer of 16, but NOT about the rest. Just relax.
Oh, and the answer is still 16. lol
Technically if you are basing that a square has no lines through it then it would be 17 squares because of the outer box. All the lines hit it perpendicular and not run through it.
The INSIDE was NEVER a square. The SQUARE IS DEFINED BY THE LINES.
This is really quite a nonsense argument.
… a grid?
http://www.math.cornell.edu/~hatcher/Top/TopNotes.pdf
Basic topology.
Kilahill is correct provided that we are to assume that the lines in the image all lie in the same plane (which I feel is the intent) and are not a projection of a third dimension, in which case 40 is a correct answer.
A square can have something inside of it, specifically a line in this matter, and still be a square. The definition doesn’t say anything about the inside of a square. If you would count the squares as you would in the diagram, then you will get 40, not 16.
Kilahill
It’s because your definition of a “real” square is flawed. There’s nothing wrong with the lines going through. A square is defined only by the lines that create it. So back to 40.
It is 16. Period. End of discussion. If you disagree, you’re an idiot.
This is meant to make you think there HAS to be a high number of squares. You’re all over thinking it! That’s the whole point to this. It is 16. I am literally the ONLY one EVER to guess 16. Am I a genius? I think so, lol.
Again, cocky, arrogant, offensive attitude, thinking that everyone has to agree with you, or they’re an idiot. You sound like my mother-in-law.
http://www.teachingideas.co.uk/maths/chess.htm http://www.basic-mathematics.com/checkerboard-puzzle.html These math websites, as well as others I’ve seen, show that in counting the squares on a checkerboard, you count all squares, yes, even those with lines through them, which would equal 204 squares total.
The definition of a square is ‘A shape having four equal length sides’. It says nothing about what is inside that shape, it only defines the sides. Therefore a square divided by any number of lines is still a square.
The answer is 40 and YOU are and Idiot.
Oh people, oh people. So angry over such a fun brain teazer! lol
Sure, they OUTSIDE shape is still a square, but, the INSIDE is broken up, making it no longer a square. It’s a square with many shapes on the INSIDE. Rendering it NOT A SQUARE ANYMORE.
I was serious about my answer of 16, but NOT serious about my attitude. I am having fun with you people. Relax a little.
Did you edit your answer? I could have sworn you said 12 (thus my comment).
Geez people kilahill was being sarcastic, not once was he demeaning! Oh and to the person that keeps calling him ‘and idiot’ it’s ‘an idiot’ I’ll refrain from calling you a dope.
I agree with Jon..and anyone else who knows the definition of a square being a shape having four equal length sides. PERIOD. The answer is 40.
If a square “has” a side, may the side belong to another? The question of side ownership also relates to separability. If you print out the diagram on paper, you cannot cut out 40 squares. So, many of the squares are imaginary. Is the task to count real squares or imaginary ones?
Hi Matt. I’m not sure I quite understand the question. A square, in geometry is defined as having all sides equal, and its interior angles all right angles. So it’s about the lines. Yes, a line can be used for one square and again for another. And it’s not about cutting anything out. It’s about finding 2 sets of 2 parallel lines that cross each other making 90 degree angles and in such a way that the four bordering segments are equal.
There are no imaginary squares here unless we’re drinking lots and tipping our laptop and holding our head at an odd angle and squinting our eyes. (this last part wasn’t directed at you).
I’m not meaning to offend you in any way.
But how do you not count the 4×4 and 2×2 squares that the diagram shows?
And you shouldn’t be calling people idiots.
I got 16 as well. Good job.
Open your mind. It’s 40. Look around and see.
It could never be 16. It would have to be 17. You have to count the entire grid. It has 4 equal sides. But the correct answer is really 40.
beejay923@gmail.com
No, you’re still wrong because your definition of a square is just….oh my god, re-take high school geometry. Please.
You’d think a site that starts out with a gif that counts the squares for idiots completely incapable of counting for themselves would end this. It’s astounding, really.
I see where they are getting more than 40 from…IF you copy and paste the image into something like microsoft word and blow it up it has little squares at the corners of the squares in images 17, 18 and 31. In fact the one I blew up has even more little squares in that. Like Tracy said though you have to tip your screen back and such. But looking at ONLY the black lines and not the little gray ones that pop up at the corners of the squares there are 40 and that is what I counted before finding this site! Hope this helps some of you!!! Have a great night!
@ Kilahill
If you are getting picky then there are only 8 squares. a square needs 4 lines, if you draw square 1 then to draw square 5 you are only drawing 3 lines so is that really a square?
square 1 and 9 can be squares or 5 and 13 and 4 and 12 or 8 and 16 then 4 of the small ones.
If squares are allowed to be drawn using sides that are already in place then this drawing can be made by drawing 29 squares that at the time of drawing do not have any other lines inside them. e.g. the 4×4 square then square 27 then 1
I just did a quick count of these 29 so there may be a way of drawing this with more than 29 squares that do not have any internal lines at the time of drawing
There is no reason to deny a square its’ shape by having other shapes or lines inside of it.
@ starknerd.
Thank you!
I got 40. I found this on facebook and decided to try it out. It took me going on to paint and pasting the puzzle square 11 times to color in all the different squares to get my number. I felt kind of stupid when I scrolled up through the comments and saw that you had pasted the answer and how to figure it out. I was fun trying though so I wasn’t to bummed. Actually I was kind of suprised how many people only got like 24 squares.
At first, I only got 19…
At first, I only got like 19… I wasn’t counting the overlapping squares.
Holly, don’t ever feel stupid about something like this – even if it takes scrolling up. It’s a mind thing, self-test in “fun”, as you said. It’s too bad more people don’t accept the fun knowledge.
I guessed 16 because I was looking for only actual visible squares and not overlaying and reusing what I had already counted. It is your perception that causes different answers to come up. So depending on the method you use and your own personal perception we are all right to some degree.
So I’d say 40 and 16 are both correct. Take a crayon, color the squares different colors as you count them and don’t reuse the colored squares and you can only come up with one answer….16. That is my reasoning. The 40 is only possible if you reuse what you have already counted.
No I disagree. You are not reusing them, they are different sizes. You are not reusing the same square at any point.
It is simply a parlor trick with more than one answer. I bet you could win money at a bar with this easily. Because no matter how they did it you could still tell them they are wrong. LOL!
No. You’re wrong. There are 40 squares.
Once again kids, squares are defined by the lines that make them, not the color in the middle, or the space in the middle. Get any geometry book or look it up online. A definition of a square is about the lines.
This isn’t a game of perception. It’s about counting 40 damn squares.
I got 40 right away then counted rectangles. 74 correct?
Every square is a rectangle. Not every rectangle is a square. We’re only looking at squares. Have a nice day :)
ok, 4o squares, 74 additional rectangles that are not squares.
I count 41 squares. Your animation misses the square encompassing your #6, 7, 10, and 11.
Crhis
Never mind; I’m an idiot. There are 40 squares after all.
OK…So you have the squares figured out….how many RECTANGLES are in the same group? No cheating!
104 rectangles so far
There are (5 choose 2)^2 + 2*(3 choose 2)^2 = 10^2 + 2*3^2 = 118 rectangles. The first term comes from choosing which of the big vertical lines are the sides of the rectangle, and which of the big horizontal lines are the top and bottom. The other term comes from asking the same question in the smaller 2×2 grids that are offset from the big lines.
This is the same approach I used to get 40 for the original problem, except the 1^2 + 2^2 + 3^2 + … + n^2 = n(n+1)(2n+1)/6 squares in an n-by-n grid are replaced by (n+1 choose 2)^2 rectangles.
Depends on what you consider a square. A square to me is shape with 4 points, and I counted 16 because of it.
Based on my definition, I am correct.
Ramik. Was that sarcasm? If so, it was funny.
On the small chance you were serious, there is no “what you consider a square.” A square has a very specific definition.
But I’m going with that your post was pointed and funny.
this is really funny. i counted 3 times and got 36 then i saw 36-39 the forth time i counted. although i have never participated in an online discussion, i find them really amusing because this really is a simple geometric puzzle and people are getting all in a rut about something so small. really, there are 40 squares, this isnt a debate, but so many people seem to be getting in a huff about it, debate something that can be debated!
Agreed. I stopped trying to explain to people and just decided to sit back and watch the shenanigans. I can’t help but laugh at people who have their own definitions of a square. Last I checked there was only one definition, and a pretty solid one at that.
I agree. “A square is a shape with 4 sides of all the same length.
Four right angles and all sides are the same length, to be exact. :)
Show me a shape with 4 equal sides that’s not a square. No?
It’s superfluous to specify the 90 degree angle requirement, since “4 sides of all the same length” must also make 4 right angles.
The shape YOU’RE thinking of is a Rhombus. A shape can very easily have 4 equal sides without having 4 equal angles. That’s why the definition of a square stands at 4 equal sides and 4 equal angles. http://en.wikipedia.org/wiki/Rhombus
Oh, and to quote from your other comment regarding a simple spelling error:
“Make sure you know what words to use if you’re trying to sound smart or you will fail.”
You were close to right at least. A triangle with 3 equal sides automatically has 3 equal angles. A rhombus however does not.
Dang, you got me there Greg. I think it was too late and I had too much gin to drink. Completely forgot about parallelograms.
And one of my pet peeves is when a person uses a whole bunch of big words to try to sound smart, but then gets a simple word wrong. It just bugs me. Kind of like when people think they know how maths work. :)
People always forget about parallelograms.
… and the Spanish Inquisition.
I have consistently found 40, but I am curious as to how anyone is finding 44. I don’t see how that works and would like to know their logic.
Hello, When counting white squares, yes, there are 40. However, think ‘outside the box’ and count both white solid squares AND black lined squares. There are two sets here, taking the total to 80.
There are no white “solid” squares. The squares ARE THE LINES NOT THE SPACE IN BETWEEN.
40 squares.
If you look at a street and are asked to count buildings, you wouldn’t also count the dead air space between. Why do people keep doing this with squares???
Holy God, whomever made this gif has WAY too much time on their hands. Furthermore, I can’t believe this “puzzle” is still going around the internet. I think I remember something like this in 2ND GRADE MATH! There is no excuse for anyone not being able to count squares.
I saw thus first on Facebook and for ages I counted 36, but then realised I’d missed the 3×3 squares. A square is a shape with 4 equal sides. A pizza is still I circle when it is cut into pieces. The Pentagon is still a pentagon even if the centre is cut with another pentagon. I think the question should be without moving any lines how many squares can you make. It’s 40, thats a logical way to work it out. No hidden squares, use the lines. How many squares can you seperate from the rest?
The shapes around the small squares in the interior have 6 sides so they are not squares. You have to ignore what you see and you have to ignore the definition of a square to count them. If you get to play psychological games to arrive at the answer you want, anything goes.
Where are there six sides???? The small squares in the interior do not have six sides. Put down the bong.
http://www.flickr.com/photos/disneywizard/7648693432/ I agree, I made this animation independently. It results in agreement – there are 40 squares.
No way are there 40! The video went back over 16 of them to get that number!!! My protest is lodged…though I may be wrong!
Shoshana;
There are no duplicates. Please see MY animation to confirm. http://www.flickr.com/photos/disneywizard/7648693432/
Shoshanna,
You are correct that you are wrong.
Hey guys
There are actually more. The trick is how many you can ‘see’. If you look at the 2 smaller squares, you will notice that around it is a square with a thick border (If you can visualize it). That creates 2 more squares, more than 40. You can also find a few more that way.
The second catch is that if you look long enough, a visual image of a square will appear at all the intersections of 4 lines. This has been documented with the right google search.
That brings the total so far to 63.
I hope someone can find more, but my google research has only gone this far. Enjoy! :)
I counted 63 by myself and wondered If I wad the only one on the net to come with that count thank you for your post^^
OOH OOH, someone just gave me a new insight. If you imagine a square that is only white (ignoring the black surrounding border) you can add ANOTHER 16 white squares. Cool!!
Take care
Bobby
First, there are 40.
Second, there are 40.
You’re playing games with the resolution of the picture–which is a fun exercise–but there are 40.
Second, there are no white squares. The lines are black. Since squares are defined by LINES, and since there are no white lines (that we can “see,” since that is the exercise), we’re again back to 40.
I think there are a whole bunch of white “lines” inside the white space, so the answer must be 2,464 squares.
Either that or someone has been “doing” a whole bunch of white lines. ;)
THANK YOU! I was getting so frustrated telling people!!
Okay, if you wanna be a technical f tard about it! There are 40. BUT If you count the Inside of the border/ the Border / Outside of the boarder, then you’ve got 120. Just saying!
Using this method, being a wise ass and all, with m-theory on dimensions, you’d have 2640 squares, but using the typical 10 dimensions you’d have 2400 squares….but this is thinking way outside the box!….
I skipped mentioning a step, but no one needs to know it!
it’s 40. i draw it manually and color-code each square and i found 4×4=1, 3×3=4,2×2=9, 1×1=18, .5x.5=8 total of 40. i still remember my grade school fun games..
Their is definitely 27
I get 11sets of 4squares +the 1 square that outlines it all which makes it 45 squares no imagination just straight count.
The answer is either 40 (as you demonstrate) or 16, depending on how “square” is defined.
The conventional definition is something like ” A plane figure with four equal straight sides and four right angles.”
Only 1, 4, 5, 8, 9, 12, 13, 16, 19, 20, 21, 22, 23, 24, 25 and 26 meet that definition, since the others have lines inside and therefore more than four right angles in the figures.
But thanks for the great demonstration
Only 1, 4, 5, 8, 9, 12, 13, 16, 19, 20, 21, 22, 23, 24, 25 and 26 meet that definition, since the others have lines inside and therefore more than four right angles in the figures.
No, this is not correct. The lines inside don’t have anything to do with the the 4 lines and their angles. They don’t negate them creating a square. If you take a piece of aluminum and cut it in such a way that all 4 sides are equal and are connected by 4 right angles and write “Eat at Joe’s” in the middle, it doesn’t suddenly mean that the sign isn’t square because there are scribbles in the middle.
The lines inside the squares are forming other objects to themselves, but any instance of two sets of parallel lines intersecting at 90 degree angles and whose lines are equal is a square. No matter what else is going on around it.
Your argument is only true if we are to assume that the image is a composition of objects projected onto a single plane for our viewing.
It does matter if there are lines “inside” the larger “squares”. The larger “squares” are not topologically equivalent to those which are smaller. What you propose would also lead to the conclusion a figure 8 is equivalent to a circle, topologically. This makes no sense if the squares are indeed supposed to lie in the same plane.
The answer is 16 unless we assume some really strange projection space.
But Bob, if you had a big circle, and there was a smaller circle inside it, does the outside one cease being a circle. No, it doesn’t. Despite the clear amount of logic, do you cease being an idiot. No, you don’t.
A circle inside of a circle is topologically different from lines intersecting inside a larger square. There is an issue with connectedness…
The question posed was “how many squares”, not “how many projections of a square” onto the image plane.
@ Bob
In a flat plane, on a piece of A4 paper, how many square shapes can you draw on the image under discussion, using different coloured pencils and only tracing along an existing line?
That is the question, plain and simple. And, Bob, as others have shown you, if you do this (colour-coding as per @Tolits post 4×4, 3×3, 2×2 sized squares etc.), you will be able to trace EXACTLY 40 SQUARES.
Why don’t you try it? It is elementary, key stage 3 Maths, and the answer is not subject to perception or interpretation, only knowledge.
Made up my own little graphic to illustrate my finding of 47 squares…
http://img96.imageshack.us/img96/8660/squaresg.gif
To clarify (as some people may refute some of my choices in what constitutes a square):
– I have decided that hollow squares count. Why? Well, if you draw 4 lines connected at four corners, that is a square (regardless of whether it’s ‘filled in’ or not). Who’s to say how thick these ‘lines’ can be?
– You kinda need to think ‘outside the box’ – pun intended – in order to count over 40. 40 seems to be a fairly obvious number of conventional squares to discover in the image.
Rather then thinking outside the box, get back in it and seal the lid please.
You’re kidding right? Putting a hole in the middle of a square you’ve already counted doesn’t make it another square. The point of the exercise is to count how many squares can be drawn with the lines provided. It has nothing to do with filling them or not filling them. What you’ve done with your image is link up rectangles.
“Who’s to say how thick these ‘lines’ can be?” That original image lays it out pretty clearly. The black lines are the rules that have been presented for this puzzle. You’re just making your own up. That’s like saying the wood grain of a basketball court should act as some sort of boundary. The lines painted on the court are pretty clearly the lines the refs want you to pay attention to.
Yeeaaahhh, ok….I get where you’re going. Make the “lines” thicker and you can grasp seven more…sorta…but naw. I’m not buyin’ it. But, thanks for participating!
I realistically stand by 16.
http://postimage.org/image/6dtek0rgv/
“Everything should be made as simple as possible, but not simpler.”
~ Albert Einstein
If you allow horizontal & vertical wrap-around there are more, & if you say allowing Horizontal and vertical wrap-around implies diagonal wrap-around too (ie, mapping onto a sphere) then there’s more again. In all, on top of the 40 already counted, you can add 12 [16-sqs] + 16 [9-sqs] + 4 [4-sqs] or additional 32 squares, making 72 total.
Of course, allowing spherical mapping thus, actually limits the number of possible plane-squares, by making the following impossible:
without wrap-around, you can add an infinity of squares, if you allow the 16-sq to also represent a 25-sq, the edges of which don’t completely show; then a 36-sq, 49-sq, etc etc. These could all be counted as part of each IS shown in the diagramme…
Plus, as someone else on FB said, add one for the WORD ‘square’ in the question. So, 73, plus.. And, a shot in the dark, maybe people familiar with 4-to-n-dimensional topology could add more by mapping the 16/18-sq onto more exotic concepts like klein bottle etc..
Did you count the 3×3 squares as well?
Did you count the 3×3 squares as well? Which would make the total higher than 40. If not, why?
Yes, if you’ll take another look at the animation above, you’ll see the four 3×3 squares account for numbers 36, 37, 38 and 39.
Did you even watch the gif at the top of the page??? Just watch it and stop asking stupid questions.
I see circles….time for zzzzzzzzzzzzz
YOU VILL SEE 40 SQUARES AND LIKE IT!!!
Either 16 or 40, depending on how you look at it…but I think that’s the point. I guess that technically there are a fair few irregular hexagons. Ooh what fun!!
When I first saw this picture on Facebook, I counted 40 squares. I don’t need any animation to tell me there are 40 four-sided figures in this picture!!
there are 44. you missed 4 in your animation.
If you have 4 equal length lines making a box with four 90 degree angles you have 1 square. You could say you have 1-squared squares.
With a 2X2 grid you would have 2-squared plus 1-squared squares which equals 5 squares, some with lines in them.
(From here on out I will write that as 2² + 1² = 5 squares.)
With a 3X3 grid you would have 3² + 2² + 1² = 14 squares.
With a 4X4 grid (like here) you would have 4² + 3² + 2² + 1² = 30 squares.
With a 5X5 grid you would have 5² + 4² + 3² + 2² +1² = 55 squares.
What we have here is a 4X4 (that’s 30 squares) and two 2X2 squares (that’s 5 each, so 10 squares) which means you have 30+5+5=40 total squares.
And now you can figure them out for other combinations.
I like Peter BJ’s suggestion. Back when I was young we played checkers. We called it 3-D checkers, but actually it was more esoteric than that. The two sides of the board were the same line. So for example, you could move diagonally forward to the right when you were already on the right side of the board — IF the correct square on the left side of the board was empty!
The two ends of the board were another same line. So for example you arrived at the next to the last row and jumped over the other’s piece he hadn’t moved yet, you didn’t land on the king row, you jumped over it (back into your own king row). We eventually decided that the rules said you had to land on the king row to become a king, so jumping over like that you didn’t become a king.
It’s two cylinders, going two directions at once, so you can’t create a board in real (3D) space. But I finally figured out that if I in my imagination copied the playing board as a 3X3 grid of checkerboards, I could jump from the center board onto one of the imaginary boards to see where my position was — but on the real (the center) board. That helped.
We never could get it to work with chess (first player has check mate without moving).
We wrote it up and sent it in to Scientific American, but never heard from them, so we sent a copy to the Library of Congress for copyright purposes but never got anybody else interested in it, so it didn’t go anywhere.
hey Jack, nice to see *someone* isn’t being dogmatic etc. See my new post below too. I was thinking, about my last idea, of connecting in a kind-of 3d spiral .. say square labelled clockwise fashion ABCD, then connect side BC with side DA, but moved so B actually connects one square down from the top of DA, kinda spirally.. But then I had a thought – say your game, you made some kind of ‘Hyper-Transport/Wormhole’ rule that allowed you to (metaphorically) bend/stretch the board so the king-line of one side could connect up with ANYWHERE on the board (that’s ‘topology’ I guess; google it if unfamiliar). Guess you’d have to think a lot about the rules involved..makes me think of those Star Wars (was it?) 3-D Chess games, sorta,.. Or of the game was virtualised on a screen rather than IRL, maybe AI could generate random wormholes (just from one square to one other random square) or major board warp (connecting a whole rank to another rank) – each event random & connection existing only for random short time, say one or two moves??.. though that would prolly require more like chess pieces to take most advantage than drafts.. and you’d prolly have to think over it carefully so the game didn’t get TOO random.. anyway, jus’ an idea. Cheers !
If you do not count squares with lines, you can’t even count the original square as there are lines running through it.
correction the lines do not run through the big square they hit it perpendicularly.
Correction, every line intersects perpendicularly on this, as with all 40 squares.
I get 40 every time but have a hard time getting others to see it. This is FABULOUS!! Thanks for taking the time to create it.
But you’re all wrong. After all, how many squares CAN’T you see? The question doesn’t ask for a number. You can see them all.
If you ask “How many squares are there?” …. that requires a number.
I tell you what. Some of the posts on here are genuinely retarded. Some will pick fault in my comment as its not is US English etc however, the puzzle is great. Squares with lines through are still squares as its the outer border which is counted. You all need to lighten up and say “yeh, this is good. It got me thinking.” ((like a gimp) for most of you)) and that you are all trying to be too clever and it really doesn’t suit any of you. The comments saying they appreciate the puzzle are much more valuable then some of yours.
40 is correct. Stop questioning it.
I think the answer is infinate as no-one seems to be counting the “squares” counting the squares. On this page I see many squares who have been TAKEN IN by counting squares thus meaning your are all “squares” who are now part of the puzzle .. hehehehe also meaning if the negative space inside a square and the posative space inside are square are squares in thier own right and you have all been taken into one of those spaces by taking part you must also be counted. Thats real math for you lol
Wow Arron. You are a meta genious. :)
Aaron. LMAO Good call!
I have to agree with you Ian. I counted 40. Did the math after I realized the number and yes it is 40. What this discussion has turned into is perception. Pretty much the two schools of Athens going on here in geometry and math. Which is absolutely appropriate, given the Greek reference. Aristotle inductive reasoning. Use the sense to establish patterns and create an absolute
Definition (simply put). Or Plato. There are Shapes and shadows that we, normal humans, are not aware off because our simple senses fail us.
I see 40 in traditional 2 dimensional math that are described, but also see a total of 57 if you count each intersection that has a full x/y cross (square black pixels at each intersection). If you count partial intersections I count 81, but traditional math dictates 40 as each line is considered to be 0 space, only used as a reference. I am no math genius, but I see 40 as described.
There is actually well over 150 there.
I got to 172 so far. im sure a second look there will show more
There is an infinite number of squares that are not demarcated by visible black lines. Just kidding. 40 is correct if you go by what is surely the spirit of the puzzle. (OK, maybe 80 if you count negative space, or 120 if you count both the outside and inside of the lines as squares in their own right. But again, the spirit of the puzzle probably doesn’t include those somewhat esoteric squares). 40 is the commonsense answer.
I would like you to know that the square middle left and middle right are not in fact squares as they have 6 edges and not four so the 40 squares is wrong
hey Christopher Kirkman, I found this picture on facebook and I have a question about it. the picture itself is square so could you consider the whole of the picture outside the lines as being square number 41?
I don’t believe that to be the intention of the puzzle. You can read back through dozens of comments here and on FB and see that people have as many explanations and answers as there are comments. However, remembering back to when I first saw this in 6th grade geometry class, I believe solving it correctly meant interpreting the question as “how many squares (4 sides of equal length) can you TRACE using the lines provided?
There are many others like this using other shapes, and although the immediate answer isn’t usually correct, the overly complicated ones people seem to fabricate so only they can appear correct are, at best, stretching things.
The truth is, the stated question is “how many squares do you see” so in essence you could scroll down for 3 pages worth of comments and count each of the squares surrounding the icons of every commenter, every checkbox, every thumbnail image and every social feed icon to get hundreds, but that’s just a little silly, don’t you think?
Aside from the clever philosophical debates and attempts at humor – I really fear for the state of mathematics in the world. There are 40 squares. Even with this flawless animation (thank you!) there is still attempted debate. Less than half of more than 200,000 posts to facebook appear to have answered it correctly. There is only one mathematical definition of a square. A planar figure 4 equal length straight sides connected and 4 right angles. Arguments concerning what is inside the square are just absurd. If you have a square driveway and draw a line bisecting it to make two rectangles – the driveway is still a square. One post defines a square as any 4 points! Still I’m encouraged that this inspires such passion from so many people. – Maybe math can make a comeback!
Another fun test – how many squares are on a Chess Board?
You aren’t alone. It astounds me not only how much traffic I’ve gotten from this little one-off post, but how many people are refuting the simple, and what I feel is pretty clear, animation.
And yes, I do find it a little disconcerting that basic mathematics principals seem to be lost on so many people. Much in the same way correct spelling is a thing of the past, especially on Facebook.
But to answer your last question, a commenter above, “Jack”, typed out the formula for figuring out how many squares can be made from any normal grid. Our up there isn’t normal, but a chess board would be, so an 8×8 board you add:
8² + 7² + 6² + 5² + 4² + 3² + 2² + 1²
and get [drumroll]….. 204.
Humans are funny animals, I witnessed a whole week of debate on talk radio about why a corn cob looks as it does after having been eaten ( the shape before and after viewed from the end ). These are the things that make one go hmmmmmm.
http://www.facebook.com/photo.php?fbid=3197347191386&set=a.1800147822275.79182.1797197068&type=1&theater
If you come on here arguing for anything other than 40 squares, it is obvious to every sane mind here that you are either-
1. Completely ignorant
2. A pretentious a** hole
3. Trying desperately to get people’s attention so they will reply to your comment
Please attempt to do the puzzle in the nature it was intended. It is obvious how this was meant to be counted, do it as such. We get it, you think you’re smart; you don’t have to prove it to strangers on some random website.
ok…none… they are all rectangles, it is an optical illusion and if you don’t believe me, measure the sides!!!! really????? a million people and no one has measured the sides!!!!
I hope that is a joke.
if you measure all the sides, they are all rectangles I see two squares of 4 blocks high and 3 blocks across that are actually squares…
When I open the image file on my computer it says the image is 2.67″ by 2.67″, meaning the length of the overall image is the same as the width of the overall image. Since all the lines are straight and parallel to the line across from it, perpendicular to the lines adjacent to it, that is one big square by definition. Next, the vertical and horizontal lines are all spaced evenly apart and placed perpendicular or to the outer square’s lines, separating the big square into 16 smaller squares (and yes, I did measure the lengths of the distances between all the crossing lines, they were all nearly exactly the same, likely off by some absurdly small inconsequential distance). The other 2 central squares (each of which can be separated into 4 additional squares) have equal lengths and widths, as well as parallel opposite sides and 90 degree angles at the corners. I honestly have know idea what you are doing to measure this, but you are clearly wrong. Terri, if you think you’re the first person in, as you say, millions of people to find out that these are not squares, you are out of your mind.
Unless you are measuring at some ridiculously small and insignificant scale just to be cute and differentiate yourself from the others, I recommend you stop measuring things with whatever tool you are using (likely the width of your thumb or placing gaps between your fingers and moving them from line to line). Be realistic here.
Thank you @LostFaith.
Just when I thought this exercise couldn’t be any more stupid, Terri proved you can take stupid to a whole new level. Well done.
In addition, to extinguish any lingering doubts (although I’m sure in your fantasy world you have to be right and I can’t convince you), I clearing out the white background, leaving just the black lines, I then duplicated the image, having the grid (with a transparent background) superimposed on the original image. I then rotated the superimposed image 90 degrees (typing in a 90 degree rotation, not by hand) and the lines of top rotated image was indistinguishable from the original image below (except the two central squares were now left and right, instead of top and bottom). If you were right, the longer lines would have stretched out beyond their underlying shorter counterparts. That did not happen, in fact, the lines didn’t even look thicker, meaning this image is really well designed and the squares are perfectly square. I understand this logic is hard to follow with a visualization, but try it your self and see. I think even simple paint programs can rotate an image and let you superimpose them. Again, definitively, you are wrong; completely and utterly wrong. I would advice you reconsider your stance, I’m sure others will take the opportunity to let you know you are wrong as well.
The shame about social media is that every idiot now has a voice, and people that should never be heard now are on a global scale. Thank you for proving my point.
Terri.
You’re an idiot. That is all.
What I don’t understand is how the middle 2 columns of squares can be counted when they are actually not squares… Because parts of them have been chopped out by the middle 2 boxes…
I do not understand everyone arguing over this.
Define square.
Those are all rectangles.
Zero squares.
Katy. Yes, they are rectangles But they are a special kind of rectangle called squares. Please continue to 6th grade before ever speaking or typing again.
@Christopher Kirkman – you haven’t commented on wrap-around. It seems a perfectly obvious thing to me since every time one types more than one line of text wrapping is used. If you (or others in here) say that wrapping implies 3D, hence disallowed, that is incorrect: when mapping a 2D (plane) figure onto a 3D figure, the ‘surface’ is still plane in itself, even though it may appear to be 3D from the 3D perspective. For example, the surface area of our planet, Earth, is measured in square miles/kilometres (plane units), even though we know the earth is, approximately, a sphere, a 3D object. Or to put it the other way, if I draw a square ABCD (clockwise) on a piece of paper: what is it’s volume? = (B-A) x (D-C) sq units. If I then curl the paper into a tube with the side AD on the side BC, and ask the same question, the answer remains the same, even if the tube of paper looks like a 3D shape. Of course you can’t physically wrap both directions, paper isn’t flexible enough, so you use theoretical (or virtual) paper, Photoshop it, so to speak, and/but the answer to the question, what is the area of the square ABCD?, is the same, in *square* (ie, plane) units.
Of course, for purposes of a junior math type question, no argument with 40. But if it were a figure in say, a physics or astronomy or etc etc* paper then the expectations might be different, and so might the results, and a simple answer of ’40’ might not be sufficient.??
just for interest: [SURFACE AREA : Volume] (ratio) is a useful thing to contemplate in some situations – (eg: http://en.wikipedia.org/wiki/Surface-area-to-volume_ratio)
@Stan K – care to comment on this (above) ?
re squares on a chessboard: I assume you mean chessboard as example of 8×8 square plane figure – in which case, drawing them all out for myself, I get:
[1×1]64 + [2×2]40 + [3×3]36 + [4×4]21 + [5×5]16 + [6×6]9 + [7×7]4 + [8×8]1 = 191.
but if wrap-around is allowed (horizontal, vertical, & diagonal),:
[1×1]64 + [2×2]50 + [3×3]64 + [4×4]52 + [5×5]56 + [6×6]49 + [7×7]28 + [8×8]29 = 392, or 201 extra over the 191.
I spent the last half-afternoon drawing all the figures – I looked, removed duplicates (hope I got them all), so this is *not* just off the top of my head.
Next part – if I did a fancy wrap, say a spiral one where top right corner wrap corner connects to one square down from top left corner..or that PLUS bottom right connects to one square along from top left.. and then varied the ‘pitch’ again after that for possibly more results… checking carefully not to include what’s already been counted… but I’ve spent long enough on this already, too long even, so if you want to work on this, good luck to you. LOL. Cheers !
i see it now! it is 40. sorry for saying you were wrong!
I now see 40 but first saw 32. I missed the one’s in the center first time.
@Peter Bay If you allow wrap around – it does become more interesting. If you take a square ABCD with side length =2m then the area is 2×2=4m^2 (obviously). You can’t compute the Volume of a 2D figure – When you wrap it into a sphere like shape (using virtual figures) you are correct the surface area is still 4. When you asked about the “Volume” I think you meant surface area. Units of length are one dimensional (like miles), Area is 2 dimensional (Square miles), Volume is 3 dimensional (Cubic Miles). If you could do the mapping of the square piece of paper onto the surface of the cube – the Surface area would be exactly 4. The cube would have a diameter of about 1.13m from S.A. = 4*pi*r^2 (integrating the Surface area yields the volume equation) V = 4/3 *pi * r^3 = 0.7524m^3 Giving a surface area to volume of 4/0.7524 = 3/r = ~5.317 for a Sphere with radius 0.564 (S.A. =4)
Regarding the basic chess board calc you had two small errors. There are 49 2×2 squares and 25 4×4 squares – for a total of 204. For an N sided board – the number of squares without wrap around is the sum of n^2 from n = 1 to N. or 1 +4 +9+16+ 25+ 36 + 49 +64 = 204 (for a chessboard) note each term is a perfect “square” (to end on a pun).
I’ll think about the wrapping aspect of a chessboard and write back on the number of squares in this case when I have more time.
Oops – I said “cube” a few times in my last post- I meant “Sphere”
theres actually little tiny lighter colored squares all over in the black lines meant to be a focus trick. I count 80.
The lines are ghost lines from a poor scan
Looking straight forward, using k.i.s.s. system, “I see” 16. No lines crossing to make squares, 8 large, 8 small, 4 shapes are not squares. The question asked was “how many squares do you see?” that question leaves it up for debate. Had the the question been worded different, and rules applied (cannot make squares crossing other lines, etc.), certainly 16 would be correct. Remove a square from the grid each time you count it and squares run out at 16. There’s an even number of squares so all the odd numbers are wrong, some are losing count and repeating. If you ask what’s the highest possible number of squares can be found, certainly 40 is the best answer as the animation points out. There are some faint lines that appear but I believe those are ghost images from a poor scan. Glass half full/empty never seems to be solved, this one may never be solved. Applying rules (math?) makes it simpler but then what’s the fun in that? ;)
lost faith…did it make you feel better to be ugly about it??? I MAY NOT BE AS CEREBRAL AS MOST ON THIS COMMENT STREAM, but I was not being mean…on my computer, with an external measuring device, the only Squares are 4 high and 3 wide, the entire pic is a rectangle… if on your computer or if you can print it and measure, you will find 40 squares. but will stick with 2 as my image is a rectangle…
I apologize for getting admittedly snappy and “ugly” in my comments. Regrettable decision. As to you seeing rectangles, I don’t know what source your image is from, but I would guess the image is distorted, or your computer/printer distorts it. Opening the file on my computer, the file stays under the dimensions set by the source I found the picture through. According to my image there are 40 squares. Again, sorry for being hateful; no real need for that kind of stuff.
Terri, you’re not as cerebral as a rock. You’re an idiot.
I’m with you Terri…It asks for squares…they are all rectangles! And initially I thought the only squares were the two shapes in the middle, but they are just off a bit too which= rectangles. It’s an optical illusion folks…
Based on an image size of 320 pixels x 320 pixels, the correct answer is 10,973,920. I don’t know why every guess is 5 orders of magnitude off… :/
Pixels come in round, square, and rectangle according to mfr design. Does that make a difference?
Not especially as I’m referring to the digital image pixel, and not to whatever rendering device one might be using.
144 squares, 40 square boxes as defined as boxes of 4 sides of equal lengths, 104 squares as defined by 104 90 degree angles and combined 144 “squares”…
My mind is killing me!!!! lol
My argument is based on first the definition of a square?:
A plane figure with four equal straight sides and four right angles. Two important points in the definition: 4 equal sides and 4 right angles.
Using this definition this eliminates many squares….from my calculation 19 but there could be other squares that fit this defintion out there…they seem to appear out of nowhere.
I see 42 squares. The Square that has a middle square, can be looked at as an empty middle, with a thick edge forming an additional square.
I see 40. This picture finally finished my quest for an answer lol how is it that someone made this game and never supplied an answer? I would also like to know why everyone still keeps arguing there is more than 40 and saying how could you post this? How could you post a comment and not thoroughly make sure your argument is a valid one?! lol good lawddd.
Ok, just wanted to write to thank you for taking the time to publish this animation, and to comment on how eerily similar our brains functioned in regards to the animation — with yours demonstrating a tad more diligence, having included the counter which I opted to leave out (due to my GIF animator not having an easy way to cleanly add one).
http://home.comcast.net/~krkweb/misc/squares.gif
What a fun game for the mind — and the kids :) I spent far too much time geometrically working through my formula only to discover what I thought were two additional squares; thus, arriving at 42. I, however, did not use highlighted animation. Entirely possible my mind double counted. Any more puzzles available???
When you draw a square and then draw lines inside that square attached to the lines of the original square, you instantly make the original square a different shape than a square. This 40 square assumption is incorrect unless you qualify that every background square should be counted. Even then that’s cheating!
I couldnt resist counting the squares.
i found 40 squares…..
I missed out the 3 x 3 squares
In my opinion, there are 16 squares. Anything beyond that is based on the assumptions that the image is layered and/or transparent. Since that’s impossible to know unless it is stated as fact along with the image, the only certain answer is 16.
Ugh, yer kidding right? You have to be. Let’s make it simple. Print out the image. Take a crayon to the paper. Now draw a horizontal line from any point on that grid to any other point in the grid on that line. then draw a vertical line to another point. then horizontal, then vertical again back to the original point. If your lines are the same length:THAT’S A SQUARE. It doesn’t matter how many other points you passed over to get from point A to point B. There’s no layering, there’s no transparency.
It’s a simple shapes puzzle for a 5th grader, why is this so difficult for everyone?
is wrong are 41 there is also a central turn of the small
OPS sorry, is counted are 40
I counted 41.
All of the squares you Identifed +1 2X2 square in the center!
Correction 40; Re-watched the video Center 2X2 counted
ridiculous, are only 17
português
inglês
espanhol
the boxes can not overlap
Thank you. I had gotten 40, also, but I was seeing people saying things like “58” on another posting, and I couldn’t for the life of me figure out what I was missing.
if you want to know how many squares are actually in the image you must not think in 3d. There are only 17 actual squares. However, if you count the ones that your mind can perceive there are 40
I think each of you will find you are in fact all wrong, the original puzzle is infact an optical illusion and when drawn properly each ‘square’ is infact a rectangle and when you turn the paper on its side only then can you see that the measurements do not match those of the descripiton of a square so the answer is 0 … hope I cleared that up a bit for people
Yeah, good one Nicole. Thanks for proving the fact that all people aren’t equal, some are stupid and shouldn’t be allowed to breed.
Your counting the outer sq As 1 but in fact if you count the twelve sq on the inside it would
Be 41…?
It’s amazing how little common sense most people have if they can’t figure out the simplest things. I guess common sense isn’t that common.
you missed a lot of the squares, please re-evaluate
Why are smart people dumbed down to name calling? I guess an increase in intelligence comes with a decrease in immaturity? Just state your case and zip it.
it amazes me how people try to “outsmart” other people with things like this. THERE IS NO SPOON PEOPLE…
There are 40 if you count the ones with black edges. There are also another 16 if you count the ones with WHITE edges (i.e. inside the black squares). I make it 56 total, but maybe I am just being picky :)
I printed out the graphic and got my scissors out. After cutting along each line I had 8 large pieces of paper and 8 smaller pieces of paper in the shape of what is traditionally known as a square. I had 8 large pieces of paper with 6 sides not a square. So in the “real” world there are only 16 squares whereas in the “virtual” world there could be 40 more or less depending on how intelligent you are, level of education you have, eye color, hair color or any number of traits you possess.
It didnt say print them out and cut them, it said look at the screen.
What about the white border outside of the entire square…. Does that not count??
And why are some of you talking about “there are only 16 true squares” etc.. Imagine them as stacked on top of one another..
THANKS for the clever easy to understand graphic! It took me forever to arrive at 40, then wanted to know if it was right. The search led to you!! Vindication!! (and no more searching for more)
You can cut out only 16 squares. How many you can count, is a nother thing, the test is to little described to know if u gna count it as a hexagram or none “destroyed” squares. 92 % here says 40, i say 40, but i understand ppl saying 16.. maybe theres just a dude fu**ing with us, he did a great success
Do you guys know and make a difference between square and rectangle my answer is 28
If you’re referring to me, the author, then yes, I know the difference. A rectangle is a four sided plane with four right angles. All squares are rectangles, but not all rectangles are squares. As laid out in the animation above, 40 squares (a plane with four EQUAL sides and four right angles) can be created using the lines provided.
I had the same issue and created my own version of your counter here:
http://youtu.be/5bMdrdcV4yM
this is about the hidden square there are 40 square the solution is ( 8×1 ) + ( 4×4 +2 ) + (3 x 3) + (2 x 2) + (1 x 1) = 8 + 18 + 9 + 4 + 1 = 40 squares
The formula n²+(n-1)²+(n-2)²… will determine the number of squares in a square arrangement. In your chessboard setup with its 8×8 arrangement the number of squares will be 8²+7²+6²+5²+4²+3²+2²+1²=204
In the picture we have a 4-square setup which then gives you 4²+3²+2²+1²=30 squares plus two 2-square setups (2²+1²)×2=10. All in all 40 squares in the picture.
putting the two squares in the middle splits those eight middle squares into 4 smaller squares each even though they are not outlined.
Jesus Christ man some people put way too much time into this (guy two comments up) Just count the squares! lol. Jk
Saw this on FB for the first time today and counted 40 the first time I tried b
Wouldn’t it be 41? The entire box is also a square.
That was the last one Terri, watch the video.
terri. that is square # 40. haha people crack me up just accept it :)
I think the problem with people using the line thickness to get more than 40 squares is that they don’t understand the representative definition of those lines. Using their logic, there would be no true squares because none of those lines is truly straight, none are truly the same length and even the angles would not be exactly 90 degrees. It would also render the ‘they’re really rectangles’ argument as false. This problem is a simple geometry problem, not something that was meant for college math majors (although I’m sure they could have more fun with it), so all the extra ‘dimensions’ being mentioned have no real place either.
I usually don’t respond to anything like this, but in this case given the idiousy of the debates and tirades against an absolute (that being 40 squares) I just can’t resist.
Does anyone remember this old maxim? “It is better to remain silent and thought a fool, then to speak up and remove all doubt.”. The End
I got it right!
44
40 is correct, but does anyone know how many rectangles?
I do.
58 or 59
I say 59
Well, there are 118 rectangles… agree?
Yea I see 40, and 42 but 16 is right. Logically a square is not a stack of cubes making a structure as a whole unless you want to count all the friggin atoms which are not square. If we allow a stack of cubes to be a larger cube then the damn things with the voids count as a squares or cubes.. or whatever you want to call it. Actually, the whole square with a square hole is in fact a square and the piece that left the void is another square. I’m thinking this debate is HOLY CRAP OVERBOARD! Let the smart people be smart :D I’m not. But there are 42 squares and 16 “real” squares.
You’re right Dave, you summed it up perfectly with the line that you are not smart. At least you are self aware, most people aren’t.
I love these games. They make me think. Usually I draw them out on graph paper. I got 40 when I drew it myself. Going over every line with different colors. I can’t find anymore. Thank You for the fun. Keep them coming. I enjoy these and number games.
Well bolter, you needed that. I just feel bad for the people that have the misfortune of being around you.
Sorry, but the solution in the video is incorrect. Since there is no information given concerning the figure as to whether any of the angles have a degree measure of 90 or as to whether any of the segments have equal lengths, there is no reason to conclude that this figure contains any squares. The only correct answer to this would be zero.
Those who claim a square is not a square based on “lines” inside do not understand that the term relates to the outside shape. Mr Bean’s image could be inside, it’s still a square – with an image inside.
tracy is a fn idiot… tilting your screen back? wtf… are you serious… you;re such an idiot.
Hey Christopher, nice animation. There still seems to be some debate though – by the dummies of course – so I’d thought I’d throw my 2 cents worth in that might make it a little clearer (even though for some it seems, this would be futile). Can you reconfigure the animation to start with the 8 small squares first, then the 2 squares that enclose those 8 before going to the other 16 singles, 9 doubles, 4 triples and then the full plate? It might help those idiots that, beyond all efforts made towards reasonably practicable assistance… still can’t get it through their thick Neolithic skulls.
And it looks like some might need the definition of a square also:
A four sided flat shape characterized by four 90 Degree angles (right angles) and four straight sides of equal length. And before you (those imbecilic, block-headed, dim-witted, simpleton clowns) try to argue the point – It doesn’t matter a fuck if there’s another line running though it or… or a fucking train for that matter! Lets also say it’s safe to assume that they are squares… without the need to debate whether they are a thousandth of a degree off true 90 degree right angles – either way… if only because the puzzle suggests they are squares by asking you how many squares there are in the first place.
If that doesn’t put the debate to rest then… well then I’m at a loss! A tougher puzzle than this one is determining how this sub-culture of humanity ever manage to walk on two legs, let alone string their mental masturbations together into words, or make an argument… and why are they breeding! Furthermore and for the love of all humanity – who in the hell is allowing this injustice to continue. We’ve come so far and yet the swelling of stupidity is still on the increase! Why?
There are only 40 squares. Squares are formed by 4 equal sides at right angels whether or not there are other lines running through those squares. Also, you cannot include rectangles because the sides of a rectangle are not equal.
How do I add a photo.. their are other squares that are left out. You know what, just check out my facebook page.. i’ll post the pictures there! (give me a little time, i’ll post them shortly after this post.) https://www.facebook.com/jon.michael.988
damn i got it right I counted 40!
One thing is for sure, Jay Oli wins “self-important dbag” of the thread! Bravo, sir, bravo!
I don’t care how many squares there are. All I know is that every time one of my friends comments on this on FB it shows up in my newsfeed again.
People, you have all debated, counted, called each other names and DEFINED a square, but NOBODY bothered to measure one of the “squares” in the diagram. A million people commented on facebook and everybody came across arrogant and self-important and tried to promote themselves as geniuses, but NOBODY measured the objects in the diagram.
The answer is ZERO squares. They are ALL rectangles!
Hi Christine,
Any fourth grader can tell you that all squares are rectangles that have four equal straight sides and four right angles. Every square is a rectangle. So yes, in this diagram, they are all rectangles, but that’s because they are all squares.
Secondly, barring any image artifacting, each of the squares depicted here all have the traits defined above. I should know, because I recreated the original Facebook image, ensuring the pixel height and width for each shape was equal. So, for example, the first 16 highlighted squares are each 80 pixels by 80 pixels. A perfect, by-the-book definition of a square.
Besides, even if I had made some error in the illustration, the point of the puzzle was never to be a trick question. It’s an exercise for looking beyond the obvious.
27. Some squarez are no longer squares.
I am pretty sure this website is where retards come to die. Everyone get out before you lose all the IQ points you have left
I believe that the black background that makes up the lines when looked at as a solid object sitting behind the white squares would also count as a square.
Because I work with illustrator and photshop I would consider these part of the visual construction but if the black space is not considerd an object then 40 it is.
This comment thread is amazing. You clearly illustrate through the use of animated GIF the CORRECT number of squares, yet people still disagree because:
1. They missed part of the animation and thus assumed you missed some squares, and felt compelled to call you out on “your” error before doublechecking.
2. They missed the lesson in Geometry that defines a square to be a regular quadrilateral (ie equal sides, equal angles), and call you out for allowing lines to overlap (by the way people those are line SEGMENTS and they still do not interfere with the squares!).
3. They fancy themselves to be mathematically erudite and want to call attention to their knowledge of non-Euclidean Geometry including the projective plane, toroids, and other esoteric facets of obscure mathematics, and thus call you out for solving this puzzle using basic elementary school knowledge.
4. They are highly suspicious of “puzzles” and are looking for the “gotcha” – i.e., include the number of pixels, oh actually they are all technically rectangles, don’t forget the outer part of the lines creates a square “different” from the inner part of the lines, the puzzle really contains an optical illusion. Thus, they call you out for trying to bamboozle them, but no! they won’t be fooled.
Thank YOU for an exceptionally clear explanation of what should be a relatively simple and classic puzzle.
0 or 8 or 16 or 40 depending on your definition of “square”. There’s quite a few rectangles, too, for that matter. If the lines are used to represent the borders which create squares, print the picture out and cut along the lines. You will be left with 16 “perfect” squares: 8 large + 8 small, with 4 leftover “L” shapes. I also see bunny rabbits and cotton candy and dead people.
You forgot to count the big square whichcontains all the smaller squares!
Care to look again Diana? The highlighted squares get progressively larger. Number 40 is the largest, encompassing all the prior squares.
Holy smokes! This is one of the longest clusterfucks of human stupidity I’ve ever seen! Watching people argue over something like this utterly compounds my complete lack of faith in this species. I’m ashamed to be a human right now. I wish I was an ape, because then I would feel smarter reading this insanely long thread if nonsense.
I don’t see any squares at all. I see dead people.
Nice! 1 Large square divided into 39 smaller squares = 40 squares.
4squared+3squared+2squared+1squared
Plus
2(2squared+1squared)
=40
I saw this on line and I counted 43! Then someone post your page saying it was 40? So my answer is why didn’t you count the three squares made up of four squares down the center?
Ok me bad!! I see it!!
Can’t believe people are still debating this..
Well… Even so sir… I found well above 40 squares… Here’s why:
4×4=16=1
4(3×3)=36
11(2×2)=44
1+16+36+44= 97 Squares is what I’v found…
But these types of problems, I guess, seem to be rigged by the original creator, whomever they are, to make it sound like anyone’s opinion is right no matter who looks at it… But this is quite the mindbender.
i get 41
I’m not sure if anyone mentioned but does’nt the written word “squares” count it is in the full picture that would make it 41 to me.
I agree! ^ ^ ^
I’ve always counted the written word ‘squares’ and apparantly the people who count that, have a more creative mind and think ‘outside the square’ so to speak. So we win!
Easy. 40 18 regulate squares, 8 little squares, 9 of 4 regular squares grouped together , 4 of 9 regulate squares grouped together and the whole thing. People say you can’t count groups as a square because of intersecting lines, but actually if you look at the groups your aren’t count the groups as a square you are counting the perimeter of the groups which is a solid line which makes the square and you not counting the same ones over because those grouped square to make bigger haven’t been counted yet.
40,according to length of sides:
1/2,8;
1:16+2=18;
2:9;
3:4;
4:1.
add up to 40.
Ha, I made the same graphic before finding this one. It’s funny I counted the squares in more or less the same order the OP did, even using red to draw the squares and white to draw the numbers. I used gimp to define the squares, saving each as a separate image, then used a script with mogrify(1) to draw the number into each image, then whirlgif to bring them all together into a single animated gif. Too funny, and apparently a waste of time on my part; result is here:
http://seriss.com/people/erco/tmp/squares-count.gif
please can someone tell me how many rectangles are here
You’ve really written a very good quality article here.
Thank you very much for sharing.
fully explained here: https://www.youtube.com/watch?v=w4HjsHUdqGg
I count 42 here on the top right you count 2 at the top of the square on on the right and one on the left but you could count 2 more on the bottom of this square one on the right and one on the left